CERAMATHS - DMATHS seminar: presentation by Niami Nasr

The CERAMATHS Mathematics Department seminar will welcome Niami Nasr (Université de St-Étienne) at 2pm, Thursday April 3, 2025, for the following talk:

Submerged boundary numerical methods for two inverse problems: one in medical imaging and the other in volcanology

Inverse problems are found in many diverse applications. The aim is to reconstruct a source within a domain from data measured on the edge of that domain. In this talk, I will present two inverse problems: one in medical imaging and the other in volcanology. For each of these problems, a numerical submerged boundary method is proposed. Why a submerged boundary method? Because, in both cases, we're dealing with problems with moving geometry, which requires remeshing steps that are numerically very costly if we use classical methods with adapted meshes. This is why we opt for an immersed boundary method, which allows an implicit implementation of the domain boundary, thus completely avoiding remeshing steps in the case of problems with moving geometry.

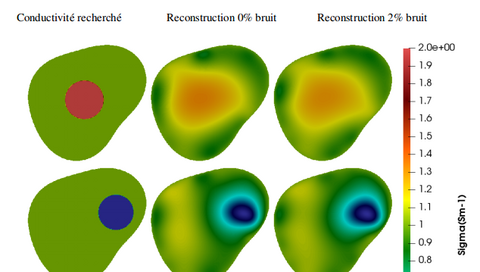
The medical imaging problem is entitled "Electrical Impedance Tomography", where the objective is to reconstruct conductivity in the volume of a domain from measurements taken on the torso using an electrode belt. For this problem, we propose a finite-difference immersed boundary method. We will discuss the convergence of this method, as well as initial sensitivity analysis studies currently being carried out for the direct problem.

The problem in volcanology aims to reconstruct the traction on sources (fractures inside the volcano), knowing the displacement field at the Earth's surface. For this problem, we will first present the state of the art, then the first steps towards an implementation of a submerged boundary method.